Answer:
0,006
Explanation:
The probability to choose 1 red ball is

The probability to choose 1 green ball is
19/98=0,19
The probability to choose 1 purple ball is
30/98=0,31
The probability to choose 1 blue ball is
24/98=0,24
We have replacement, so to choose for example 1 red ball at first is 0,25, and to choose again red ball is also 0,25. (Those are two independent events)
The probability to choose 2 red balls, 5 green balls, 10 purple balls and 5 blue balls (in this order) is:
0,25^2 x 0,19^5 x 0,31^10 x 0,24^5=0,065x0,0013x0,0000082x0,0008=55432e-13 (calculation)
But in question we don’t have order, we know just number of balls. So, we need to know how many orders we have with 2 red, 5 green, 10 purple and 5 blue balls. This is permutation with repeat. The number of orders is
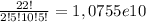 (calculation)
(calculation)
So the answer is 55432e-13 x 1.0755e10=0,006 (claculation)
I’m not sure about calculation, but in the form of the answer i’m sure:)