Question

A new potential heart medicine, code-named X-281, is being tested by a pharmaceutical company, Pharma-pill. As a research technician at Pharma-pill, you are told that X-281 is a monoprotic weak acid, but because of security concerns, the actual chemical formula must remain top secret. The company is interested in the drug's KaKaK_a value because only the dissociated form of the chemical is active in preventing cholesterol buildup in arteries. To find the pKapKapKa of X-281, you prepare a 0.079 MM test solution of X-281. The pH of the solution is determined to be 2.70. What is the pKapKapKa of X-281

Answer 1

The
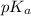`pK_a` of the X-281 medicne is 4.29.

Step-by-step explanation:

Concentration of medicine in solution =
`[HA]=c=0.079 M`

`HA\rightleftharpoons A^+H^+`

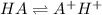
Initially

c 0 0

At equilibrium

(c-x) x x

The expression of an dissociation constant
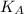`K_A` is given by :

`K_a=([A^-][H^+])/([HA])`

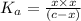`K_a=(x* x)/((c-x))`..[1]

The pH of the solution = 2.70

`pH=-\log[H^+]`

`2.70=-\log[H^+]=-\log[x]`

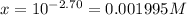`x=10^(-2.70)=0.001995 M`..[2]

Using [2] in [1]

`K_a=(0.001995 M* 0.001995 M)/((0.079-0.001995 M))`

`K_a=5.170* 10^(-5)`

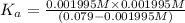
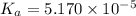
The
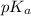`pK_a` of the medicine :

`pK_a=-\log[K_a]=-\log[5.170* 10^(-5)]=4.29`

The
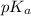`pK_a` of the X-281 medicne is 4.29.