Question

The test statistic for the HR manager's hypothesis test about the mean number of recorded participants is 13.86. The critical value is −1.751. The rejection region is left-tailed. Conclude whether to reject or not reject H0, and interpret the results

Answer 1

We conclude that null hypothesis is not rejected.

Explanation:

We are given that the test statistic for the HR manager's hypothesis test about the mean number of recorded participants is 13.86. The critical value is −1.751.

Also, it is provided that rejection region is left-tailed.

So, our decision on whether to reject or not reject our null hypothesis (
`H_0`) based on the rejection region is given by;

Since, it is know that distribution is left-tailed, so;

If the critical value is less than than the test statistics, then we will fail to reject null hypothesis and ready to accept it.

If the critical value is more than than the test statistics, then we will reject null hypothesis as it will fall in rejection region.

So, according to our question;

Critical value = -1.751

Test statistics = 13.86

Clearly, it can be seen that critical value is less than than the test statistics, so we will fail to reject null hypothesis and ready to accept it.

Therefore, we conclude that null hypothesis
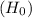`(H_0)` is not rejected.

Answer 2

We fail to reject the null hypothesis and accept it.

Explanation:

We are given the following in the question:

Hypothesis:

Mean number of recorded participants

Calculated test statistic = 13.86

Critical value = -1.751

We are conducting a left tailed hypothesis.

Rejection region:

If the calculate test statistic is less than the critical value, we fail to accept the null hypothesis and reject it.

We accept the alternate hypothesis.

Since,

`13.86 > -1.751`

We fail to reject the null hypothesis and accept it. Thus, the test result are not statistically significant and and at best provide weak evidence against the null hypothesis.