Question

Write the equation of the circle whose diameter has endpoints (-16, -16) and (-4, -8). *

Answer 1

The equation of circle is
`(x+10)^(2)` +
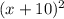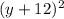`(y+12)^(2)` = 52

Explanation:

Given the endpoints of diameter of a circle: (-16,-16) and (-4,-8)

We know that the equation of circle is given by

`(x-h)^(2)` +
`(y-k)^(2)` =
`r^(2)`

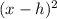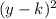where (x,y) is any point on the circle, (h,k) is center of the circle and r is radius of circle.

To find (h,k): the center is midpoint of diameter

Midpoint of diameter with end points (x1,y1) and (x2,y2) is given by

(
`(x1+x2)/(2)` ,
`(y1+y2)/(2)` )

(
`(-16-4)/(2)` ,
`(-16-8)/(2)` )

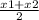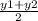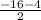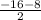(-10, -12)

Hence (h,k) is (-10,-12)

Substituting values of (h.k) and (x.y) as (-10,-12) and (-4,-8) respectively in equation of circle, we get

`(-4+10)^(2)` +
`(-8+12)^(2)` =
`r^(2)`

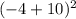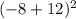`r^(2)` = 52

Substituting values of (h.k) and
`r^(2)`, we get the equation of circle as

`(x+10)^(2)` +
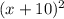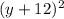`(y+12)^(2)` = 52

Hence the equation of circle is
`(x+10)^(2)` +
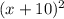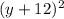`(y+12)^(2)` = 52