Answer:

Step-by-step explanation:
Hello,
In this case, it is convenient to state the ideal gas law in terms of the undergoing change due to the chemical reaction:
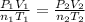
Since no volume change is present, one obtains:

Thus, it is possible to assume that the moles of hydrogen and oxygen are 2 mole and 1 mole respectively, in order to respect the given ratio, thus, the yielded moles of water turns out:

It is important to notice that just the 85.0% of the theoretical moles are actually produced, thus:
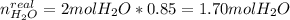
In such a way, there is a remaining amount of hydrogen and oxygen that are computed via:
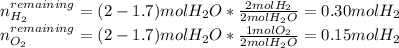
Thus, since the initial volume is:
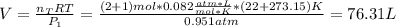
And it is conserved, at the new temperature, the pressure is:
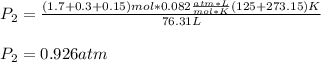
Best regards.