Question

Sickle cell anemia is a genetic blood disorder where red blood cells lose their flexibility and assume an abnormal, rigid, "sickle" shape, which results in a risk of various complications. If both parents are carriers of the disease, then a child has a 25% chance of having the disease, 50% chance of being a carrier, and 25% chance of neither having the disease nor being a carrier. If two parents who are carriers of the disease have 3 children, what is the probability that two will have the disease?

Answer 1

The probability that two will have the disease is 0.1406.

Step-by-step explanation:

Let X = number of children having the disease.

The probability of a children having the disease is, p = 0.25.

The number of children a couple has, n = 3.

A children having the disease is independent of the others.

The random variable X follows a Binomial distribution with parameters n = 3 and p = 0.25.

The probability mass function of the binomial random variable X is:

`P(X=x)={3\choose x}0.25^(x)(1-0.25)^(3-x);\ x=0,1,2,3...`

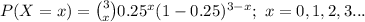
Compute the probability that of the 3 children, 2 will have the disease is:

`P(X=2)={3\choose 2}0.25^(2)(1-0.25)^(3-2)\\=3* 0.0625* 0.75\\=0.140625\\\approx0.1406`

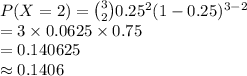
Thus, the probability that two will have the disease is 0.1406.