Answer:
84.13% of salaries are at least $74,000.
Explanation:
We are given that Professors at a local university earn an average salary of $80,000 with a standard deviation of $6,000. The salary distribution is approximately bell-shaped.
Let X = Percentage of Salary
So, X ~ N(
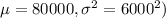 )
)
Now, the z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean
= population mean
 = standard deviation
= standard deviation
So, Percentage of salaries that are at least $74,000 is given by = P(X
 $74,000)
$74,000)
P(X
 74,000) = P(
74,000) = P(


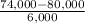 ) = P(Z
) = P(Z
 -1) = P(Z
-1) = P(Z
 1)
1)
= 0.84134 {using z table}
Therefore, 84.13% of salaries that are at least $74,000.