Question

A certain superconducting magnet in the form of a solenoid of length 0.26 m can generate a magnetic field of 7.5 T in its core when its coils carry a current of 80 A. The windings, made of a niobium-titanium alloy, must be cooled to 4.2 K. Find the number of turns in the solenoid.

Answer 1

Therefore

Number of turns in the solenoid is 19407.

Step-by-step explanation:

Given:

Strength magnetic field at its center,

B = 7.5 T

length of solenoid = l = 0.26 m

Current, I = 80 A

To Find:

Turn = N = ?

Solution:

If N is the number of turns in the length, the total current through the rectangle is NI. Therefore, Ampere’s law applied to this path gives

`\int {B} \, ds= Bl=\mu_(0)NI`

Therefore,

`B =(\mu_(0)NI)/(l)`

Where,

B = Strength of magnetic field

l = Length of solenoid

N = Number of turns

I = Current

`\mu_(0)=Permeability\ in\ free\ space=4\pi* 10^(-7)\ Tm/A`

`N=(Bl)/(\mu_(0)I)`

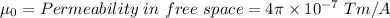
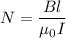
Substituting the values we get

`N=(7.5* 0.26)/(4\pi* 10^(-7)* 80)=19406.84=19407`

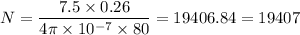
Therefore

Number of turns in the solenoid is 19407.