Question

If N = , r = , and n = , and assuming that X has a hypergeometric probability distribution, compute the following. Write your answers as fractions. (a) P(X = 2) =ans7 (b) P(X ≤ 1) =ans8 Click if you would like to Show Work for this question:

Answer 1

(a) The value of P (X = 2) is 0.3571.

(b) The value of P (X ≤ 1) is 0.5952.

Explanation:

A Hypergeometric distribution is used to describe the probability distribution of x successes in n random draws from a population of size N that contains exactly r items that are considered as success. In this distribution each draw results in either a success or a failure.

The probability mass function of Hypergeometric distribution is:

`P(X=x)=\frac{{r\choose x}{N-r\choose n-x}}{{N\choose n}}`

Given:

N = 9

r = 3

n = 4

(a)

Compute the value of P (X = 2) as follows:

`P(X=2)=\frac{{3\choose 2}{9-3\choose 4-2}}{{9\choose 4}}=(3* 15)/(126)=0.3571`

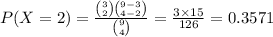
Thus, the value of P (X = 2) is 0.3571.

(b)

Compute the value of P (X ≤ 1) as follows:

P (X ≤ 1) = P (X = 0) + P (X = 1)

`=\frac{{3\choose 0}{9-3\choose 4-0}}{{9\choose 4}}+\frac{{3\choose 1}{9-3\choose 4-1}}{{9\choose 4}}\\=0.1190+0.4762\\=0.5952`

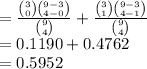
Thus, the value of P (X ≤ 1) is 0.5952.