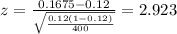Question

The percentage of adults who currently play chess (at least once during the past year) is 12% in the UK. Suppose that in a random sample of n = 400 UK residents, 67 of them play chess. What is the population parameter? What is the sample statistic

Answer 1

p represent the population parameter , true proportion of people who play chess in the UK

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

`z=\frac{0.1675 -0.12}{\sqrt{(0.12(1-0.12))/(400)}}=2.923`

Explanation:

Data given and notation

n=400 represent the random sample taken

X=67 represent the people who play chess

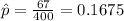`\hat p=(67)/(400)=0.1675` estimated proportion of people who play chess

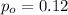`p_o=0.12` is the value that we want to test

z would represent the statistic (variable of interest)

`p_v` represent the p value (variable of interest)

p represent the population parameter , true proportion of people who play chess in the UK

Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that the true proportion i higher than 0.13.:

Null hypothesis:
`p \leq 0.12`

Alternative hypothesis:
`p > 0.12`

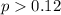
When we conduct a proportion test we need to use the z statisitc, and the is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
`\hat p` is significantly different from a hypothesized value
`p_o`.

Calculate the statistic

Since we have all the info required we can replace in formula (1) like this:

`z=\frac{0.1675 -0.12}{\sqrt{(0.12(1-0.12))/(400)}}=2.923`