Question

A uniform hollow spherical ball of mass 1.75 kg and radius 40.0 cm rolls without slipping up a ramp that rises at 30.0° above the horizontal. The speed of the ball at the base of the ramp is 2.63 m/s. (a) While the ball is moving up the ramp, find the magnitude of the acceleration of its center of mass.

Answer 1

The acceleration of the ball's center of mass = 2.94 m/s²

Step-by-step explanation:

The speed of the ball at the base of the ramp, v = 2.63 m/s

Mass of the ball = 1.75 kg

Radius of the ball, R = 40 cm = 0.4 m

In this motion, potential energy due to the height of the ball is converted to linear angular kinetic energy

Based on the law of energy conservation

Potential energy = Linear KE + angular KE

KE = kinetic Energy

Linear KE = 0.5 mv²

Linear KE = 0.5 * 1.75 * 2.63²

Linear KE = 6.052 J

Angular KE = 0.5 Iω²

I = 2/ 3 MR² = 0.667 * 1.75 * 0.4²

I = 0.187 N.s

ω = V/R = 2.63/0.4

ω = 6.575 Rad/s

Angular KE = 0.5 * 0.187 * 6.575²

Angular KE = 4.04 J

PE = mgh = 1.75 * 9.8 * h = 17.15h

Using the law of energy conservation

17.15h = 6.052 + 4.04

h = 10.092/17.15

h = 0.589 m

`h = Ssin \theta\\S = h/sin \theta\\S = 0.589/sin30\\S = 1.178 m\\`

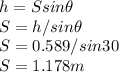
Using the equation of motion

`v^(2) = u^(2) + 2as\\2.63^(2) = 0^(2) + 2a(1.178)\\6.917 =2.356a\\a = 6.917/2.356\\a =2.94 m/s^(2)`