Question

You conduct a simulation regarding which team spectators at a football game support. Your null hypothesis is that there are equal proportions of people supporting the home team and the visiting team. Your alternative hypothesis is that there is a higher proportion of people supporting the home team. You determine that the results of your simulation have a p-value of 0.002. What does this mean?

Answer 1

As the p-value is too small the null hypothesis will be rejected concluding that there is a higher proportion of people supporting the home team.

Explanation:

The hypothesis to determine which team spectators at a football game support is:

H₀: There are equal proportions of people supporting the home team and the visiting team, i.e. p₁ = p₂.

Hₐ: There is a higher proportion of people supporting the home team than the visiting team, i.e. p₁ > p₂.

A z-test for difference between proportions can be used to perform the test.

The test statistic is:

`z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{P(1-P)(1)/(n_(1))+(1)/(n_(2))}}}`

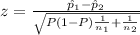
Th decision rule is:

If the p-value of the test is less than the significance level α then the null hypothesis will be rejected and vice-versa.

The commonly used significance levels are 0.01, 0.05 and 0.10.

The p-value of the test is computed as, p = 0.002.

The p-value of the test is less than all the significance level.

Thus, the null hypothesis will be rejected at any of the three significance level.

Conclusion:

As the p-value is too small the null hypothesis will be rejected concluding that there is a higher proportion of people supporting the home team.