Question

The arrivals of clients at a service firm in Santa Clara is a random variable from Poisson distribution with rate 2 arrivals per hour. What is the probability that in one hour more than 5 clients arrive

Answer 1

Probability that in one hour more than 5 clients arrive is 0.0166.

Explanation:

We are given that the arrivals of clients at a service firm in Santa Clara is a random variable from Poisson distribution with rate 2 arrivals per hour.

The Poisson distribution is foe random variable is given by;

`P(X=x) = (e^(-\lambda) * \lambda^(x) )/(x!) ; x = 0,1,2,3,....`

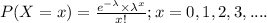
where,
`\lambda` = rate of arrival per hour =2

Let X = Arrival of clients

So, Probability that in one hour more than 5 clients arrive = P(X > 5)

P(X > 5) =
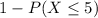
`1-P(X \leq 5)`

P(X
`\leq` 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)

=
`(e^(-2) * 2^(0) )/(0!) +(e^(-2) * 2^(1) )/(1!) +(e^(-2) * 2^(2) )/(2!) +(e^(-2) * 2^(3) )/(3!) +(e^(-2) * 2^(4) )/(4!) +(e^(-2) * 2^(5) )/(5!)`

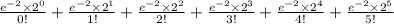
= 0.1353 + 0.2707 + 0.2707 + 0.1804 + 0.0902 + 0.0361

= 0.9834

So, P(X > 5) =
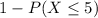`1-P(X \leq 5)` = 1 - 0.9834 = 0.0166

Therefore, probability that in one hour more than 5 clients arrive is 0.0166.

Answer 2

1.76% probability that in one hour more than 5 clients arrive

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

The arrivals of clients at a service firm in Santa Clara is a random variable from Poisson distribution with rate 2 arrivals per hour.

This means that
`\mu = 2`

What is the probability that in one hour more than 5 clients arrive

Either 5 or less clients arrive, or more than 5 do. The sum of the probabilities of these events is decimal 1. So

`P(X \leq 5) + P(X > 5) = 1`

We want P(X > 5). So

`P(X > 5) = 1 - P(X \leq 5)`

In which

`P(X \leq 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-2)*2^(0))/((0)!) = 0.1353`

`P(X = 1) = (e^(-2)*2^(1))/((1)!) = 0.2707`

`P(X = 2) = (e^(-2)*2^(2))/((2)!) = 0.2707`

`P(X = 3) = (e^(-2)*2^(3))/((3)!) = 0.1804`

`P(X = 4) = (e^(-2)*2^(4))/((4)!) = 0.0902`

`P(X = 5) = (e^(-2)*2^(5))/((5)!) = 0.0361`

`P(X \leq 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 0.1353 + 0.2702 + 0.2702 + 0.1804 + 0.0902 + 0.0361 = 0.9824`

`P(X > 5) = 1 - P(X \leq 5) = 1 - 0.9824 = 0.0176`

1.76% probability that in one hour more than 5 clients arrive