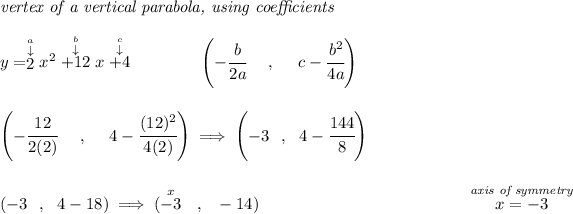Question

Find the axis of symmetry and the vertex of the graph of the function.
g(x) = 2x^2+12x+4

Answer 1

so hmmm from the equation we can see that is in "x terms" so the independent variable is "x", that tells us the parabola is a vertical one, leading term's coefficient is "2", that means it opens upwards like a bowl.

on a vertical parabola the axis of symmetry is the x-coordinate of its vertex, let's find the vertex of this one.

`\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{2}x^2\stackrel{\stackrel{b}{\downarrow }}{+12}x\stackrel{\stackrel{c}{\downarrow }}{+4} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left(-\cfrac{ 12}{2(2)}~~~~ ,~~~~ 4-\cfrac{ (12)^2}{4(2)}\right)\implies \left( -3~~,~~4-\cfrac{144}{8} \right) \\\\\\ (-3~~,~~4-18)\implies (\stackrel{x}{-3}~~,~~-14)~\hfill \stackrel{\textit{axis of symmetry}}{x=-3}`