Question

The director of the library calculates that 29% of the library's collection is checked out. If the director is right, what is the probability that the proportion of books checked out in a sample of 412 books would differ from the population proportion by less than 4%? Round your answer to four decimal places.

Answer 1

The probability that the proportion of books checked out in a sample of 412 books would differ from the population proportion by less than 4% is P=0.9255.

Explanation:

The population's proportion is
`\pi=0.29`

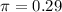
If we take a sample of 412 books (n=412), we have a standard deviation of the sampling distribution of:

`\sigma_M=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.29*0.71)/(412)}=√(0.0005) =0.0224`

We have to calculate the probabilty that the sample proportion will be between 0.25 and 0.33.

`z_1=(0.25-0.29)/0.0224=-0.04/0.0224=-1.7857\\\\z_2=1.7857\\\\\\P(0.25<\hat{p}<0.33)=P(-1.7857<z<1.7857)\\\\P(0.25<\hat{p}<0.33)=P(z<1.7857)-P(z<-1.7857)\\\\P(0.25<\hat{p}<0.33)=0.9629-0.0371=0.9255`