Answer:
The speed of the particle is
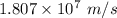 .
.
Step-by-step explanation:
Given:
Mass of the alpha-particle (m) = 6.64 × 10⁻²⁷ kg
Charge of the particle (q) = 3.2 × 10⁻¹⁹ C
Magnitude of magnetic field (B) = 1.5 T
Radius of the circular path (r) = 25 cm = 0.25 m [1 cm = 0.01 m]
Speed of the particle (v) = ?
We know that, when a charged particle enters a uniform magnetic field, the path traced by the charged particle is circular and the radius of the circular path is given by the formula:
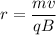
Expressing the above formula in terms of 'v', we get:
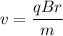
Now, plug in the values given and solve for 'v'. This gives,
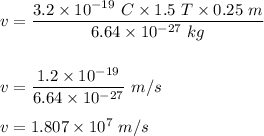
Therefore, the speed of the particle is
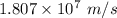 .
.