Question

An insurer uses the Poisson distribution with mean of 4 as the model for the number of claims per month on a particular policy. Each claim results in a payment of 1 by the insurer. Find the probability that the total payment by the insurer in a given month is less than one standard deviation above the mean monthly payment.

Answer 1

The probability that the insurer in a given month is less than one standard deviation above the mean monthly paymeent is 0.7851

Explanation:

The mean monthly payment is 4, and the standard devitation, by virtue of being a Poisson distribution is √4 = 2. Thus, we want to know the probability of X being less than 6, where X is the total montlhy payment.

Note that P(X<6) = P(X=0) + P(X=1) + P(X=2)+ P(X=3)+P(X=4)+P(X=5)

Also

`P(X=k) = (e^(-4)4^k )/(k!)`

Therefore,

P(X = 0) = e^{-4} * 1

P(X=1) = e^{-4} * 4

P(X=2) = e^{-4} * 4²/2 = e^{-4}*8

P(X=3) = e^{-4} * 4³/3! = e^{-4}*32/3

P(X=4) = e^{-4} * 4⁴/4! = e^{-4} * 32/3

P(X=5) = e^{-4} * 4⁵/5! = e^{-4} * 128/15

As a result

`P(X<6) = e^(-4) *(1 + 4 + 8+32/3+32/3+128/15) = e^(-4) * 643/15 = 0.7851`

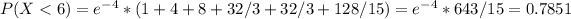
We conclude that the probability that the insurer in a given month is less than one standard deviation above the mean monthly paymeent is 0.7851