Question

The inside rail of a running track consists of a rectangle with a

semicircle at each end as shown above. Find the approximate
distance in meters for one complete lap around the track.

Answer 1

The distance for one complete lap around the track is 182.83 meters.

Explanation:

Step 1:

In order to calculate the distance in meters for one lap, we must determine the perimeter of the given shape. To calculate the perimeter of the shape, we only include the external surfaces of the shape.

The width sides of the rectangle are not included as they are interior surfaces.

Step 2:

The perimeter of a rectangle is the sum of all the sides.

As only the length sides of the rectangle are included,

The perimeter of the rectangle part of the track
`= 60 + 60 = 120.`

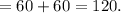
The perimeter of a circle is 2π times its radius. The given semicircles have diameters of 20 m each.

As there are two semicircles, the sum of their perimeters will equal the perimeter of an entire circle with radius 10m.

The perimeter of a circle with radius 10 m
`=2\pi r= 2 (3.1415)(10)= 62.83.`

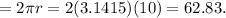
Step 3:

The total distance of the track = The perimeter of the rectangle + the perimeter of the circle.

The total distance for one complete lap
`= 120 + 62.83 = 182.83.`

So the distance for one complete lap around the track is 182.83 meters.