Question

Given that x is a hypergeometric random variable with Nequals10​, nequals4​, and requals6​, complete parts a through d. a. Compute ​P(xequals1​). ​P(xequals1​)equals . 114 ​(Round to three decimal places as​ needed.) by. Compute ​P(x equals 0​). ​P(xequals 0​)equals . 005 ​(Rounded to three decimal places as​ needed.) c. Compute ​P(xequals3​). ​P(xequals3​)equals . 381 ​(Round to three decimal places as​ needed.) d. Compute ​P(xgreater than or equals5​). ​P(xgreater than or equals5​)equals nothing ​(Round to three decimal places as​ needed.)

Answer 1

a. 0.114

b. 0.005

c. 0.381

d. 0.00

Explanation:

If x follows a hypergeometric distribution, the probability that x is equal to k is calculated as:

`P(x=k)=((rCk)*((N-r)C(n-k)))/(NCn)`

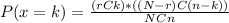
Where k≤r and n-k≤N-r, Additionally:

`aCb=(a!)/(b!(a-b)!)`

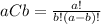
So, replacing N by 10, n by 4 and r by 6, we get:

`P(x=k)=(6Ck*((10-6)C(4-k)))/(10C4)=(6Ck*(4C(4-k)))/(10C4)`

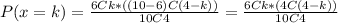
Then, the probability that x is equal to 1, P(x=1) is:

`P(x=1)=(6C1*4C3)/(10C4)=0.114`

The probability that x is equal to 0, P(x=0) is:

`P(x=0)=(6C0*4C4)/(10C4)=0.005`

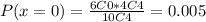
The probability that x is equal to 3, P(x=3) is:

`P(x=3)=(6C3*4C1)/(10C4)=0.381`

Finally, in this case, x can take values from 0 to 4, so the probability that x is greater or equals to 5 is zero.