Answer:
Explanation:
First group your x terms and your y terms together, move the constant over to the other side of the equals sign, and then complete the square on each set.
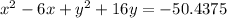
Completing the square on the x terms:
Take half the linear term, square it and add that squared number to both sides. Our linear term is 6. Half of 6 is 3, and 3 squared is 9, so we add in 9 on both sides.
Completing the square on the y terms:
Half of 16 is 8, and 8 squared is 64, so we add in 64 to both sides.
That gives us:
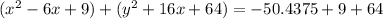
The purpose of completing the square is to create a perfect square binomial for each set of parenthesis. It will be in these sets of parenthesis that we find our center.

This means that center of the circle is located at (3, -8)