Question

P is the pressure in atmospheres (atm), V is the volume in liters (L), n is the number of moles, R is the gas constant (0.0821 L∙atm/(mol∙K)), and T is the temperature in Kelvins (K). Consider the following conditions: a sample of neon gas was under 3.0 atm of pressure, a volume of 570 mL with a temperature of 75 °C. Assume you are going to use the ideal gas law to solve for the unknown variable. What variable are you solving for? Are all of variables in the correct units? If not, which variable needs to be converted to the correct units?

Answer 1

The mass of the neon gas m = 1.214 kg

Step-by-step explanation:

Pressure = 3 atm = 304 k pa

Volume = 0.57 L = 0.00057
`m^(3)`

Temperature = 75 °c = 348 K

Universal gas constant = 0.0821
`(L . atm)/(mol K)`

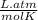
We have to change the unit of this constant. it may be written as

Universal gas constant = 8.314
`(KJ)/(mol K)`

Gas constant for neon =
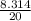`(8.314)/(20)` = 0.41
`(KJ)/(kg K)`

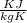
From ideal gas equation,

P V = m R T ------- (1)

We have all the variables except m. so we have to solve this equation for mass (m).

⇒ 304 ×
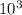`10^(3)` × 0.00057 = m × 0.41 × 348

⇒ 173.28 = 142.68 × m

⇒ m = 1.214 kg

This is the mass of the neon gas.