Question

A muon is a short-lived particle. It is found experimentally that muonsmoving at speed 0.9ccan travel about 1500 meters between the time they areproduced and the time that they decay.(a) How long does it take the muon to travel this distance?(b) How much time elapses in the muon’s rest frame (the reference frame inwhich the muon is at rest)?

Answer 1

a)
`t=5.5\mu s`

b)
`\Delta t'=12.5\mu s`

Step-by-step explanation:

a) Let's use the constant velocity equation:

`v=(\Delta x)/(\Delta t)`

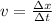
• v is the speed of the muon. 0.9*c
• c is the speed of light 3*10⁸ m/s

`t=(\Delta x)/(v)=(1500)/(0.9*(3*10^(8)))`

`t=5.5\mu s`

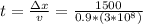
b) Here we need to use Lorentz factor because the speed of the muon is relativistic. Hence the time in the rest frame is the product of the Lorentz factor times the time in the inertial frame.

`\Delta t'=\gamma\Delta t`

`\gamma =\frac{1}{\sqrt{1-(v^(2))/(c^(2))}}`

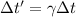
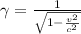
v is the speed of muon (0.9c)

Therefore the time in the rest frame will be:

`\Delta t'=\frac{1}{\sqrt{1-((0.9c)^(2))/(c^(2))}}\Delta t`

`\Delta t'=\frac{1}{\sqrt{1-0.9^(2)}}\Delta t`

`\Delta t'=(1)/(0.44)\Delta t`

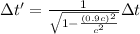
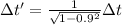
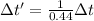
No we use the value of Δt calculated in a)

`\Delta t'=2.27*5.5=12.5\mu s`

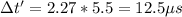
I hope it helps you!