Answer:
see explanation↓
Explanation:
We are given the following equation of a line:
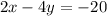
To determine the x-intercept we must set "y = 0":
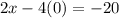

Now, we divide both sides by 2:
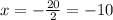
Therefore, the "x" intercept is -10.
To determine the y-intercept we set "x = 0":
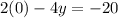

Now, we divide both sides by -4:
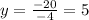
Therefore the y-intercept is 5.