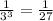Answer:
The maximum value is 1/27 and the minimum value is 0.
Explanation:
Note that the given function is equal to
 then it means that it is positive i.e
then it means that it is positive i.e
 .
.
Consider the function
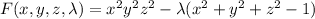
We want that the gradient of this function is equal to zero. That is (the calculations in between are omitted)

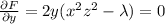
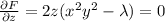
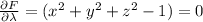
Note that the last equation is our restriction. The restriction guarantees us that at least one of the variables is non-zero. We've got 3 options, either 1, 2 or none of them are zero.
If any of them is zero, we have that the value of the original function is 0. We just need to check that there exists a value for lambda.
Suppose that x is zero. Then, from the second and third equation we have that
 . If lambda is not zero, then y =z. But, since
. If lambda is not zero, then y =z. But, since
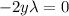 and lambda is not zero, this implies that x=y=z=0 which is not possible. This proofs that if one of the variables is 0, then lambda is zero. So, having one or two variables equal to zero are feasible solutions for the problem.
and lambda is not zero, this implies that x=y=z=0 which is not possible. This proofs that if one of the variables is 0, then lambda is zero. So, having one or two variables equal to zero are feasible solutions for the problem.
Suppose that only x is zero, then we have the solution set
 .
.
If both x,y are zero, then we have the solution set
 . We can find the different solution sets by choosing the variables that are set to zero.
. We can find the different solution sets by choosing the variables that are set to zero.
NOw, suppose that none of the variables are zero.
From the first and second equation we have that
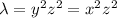 which implies
which implies
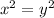
Also, from the first and third equation we have that
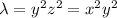 which implies
which implies
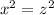
So, in this case, replacing this in the restriction we have
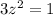 , which gives as another solution set. On this set, we have
, which gives as another solution set. On this set, we have
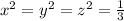 . Over this solution set, we have that the value of our function is
. Over this solution set, we have that the value of our function is