Question

At 25 ∘ C , the equilibrium partial pressures for the reaction 3 A ( g ) + 4 B ( g ) − ⇀ ↽ − 2 C ( g ) + 3 D ( g ) were found to be P A = 5.70 atm, P B = 4.00 atm, P C = 4.22 atm, and P D = 5.52 atm. What is the standard change in Gibbs free energy of this reaction at 25 ∘ C ?

Answer 1

To calculate the standard change in Gibbs free energy of a reaction at 25°C, use the equation ΔG° = -RTlnK, where R is the ideal gas constant, T is the temperature in Kelvin, and K is the equilibrium constant. Use the given equilibrium partial pressures to find the equilibrium constant (K) and then substitute it into the equation to find the standard change in Gibbs free energy of the reaction.

Step-by-step explanation:

To calculate the standard change in Gibbs free energy (ΔG°) of a reaction at 25°C, we can use the equation ΔG° = -RTlnK, where R is the ideal gas constant (8.314 J/mol·K), T is the temperature in Kelvin (25+273 = 298 K), and K is the equilibrium constant.

From the given information, we can determine the equilibrium partial pressures of A, B, C, and D. We then use these values to calculate the equilibrium constant (K) using the equation K = (P_C)^(-2) * (P_D)^3 / (P_A)^3 * (P_B)^4.

Finally, we can substitute the equilibrium constant (K) into the equation ΔG° = -RTlnK to find the standard change in Gibbs free energy of the reaction.

Answer 2

Answer: The standard Gibbs free energy of the given reaction is 6.84 kJ

Step-by-step explanation:

For the given chemical equation:

`3A(g)+4B(g)\rightleftharpoons 2C(g)+3D(g)`

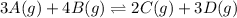
The expression of
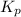`K_p` for above equation follows:

`K_p=((p_C)^2* (p_D)^3)/((p_A)^3* (p_B)^4)`

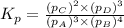
We are given:

`(p_A)_(eq)=5.70atm\\(p_B)_(eq)=4.00atm\\(p_C)_(eq)=4.22atm\\(p_D)_(eq)=5.52atm`

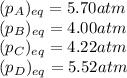
Putting values in above expression, we get:

`K_p=((4.22)^2* (5.52)^3)/((5.70)^3* (4.00)^4)\\\\K_p=0.0632`

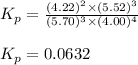
To calculate the equilibrium constant (at 25°C) for given value of Gibbs free energy, we use the relation:

`\Delta G^o=-RT\ln K_(eq)`

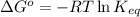
where,

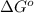`\Delta G^o` = standard Gibbs free energy = ?

R = Gas constant = 8.314 J/K mol

T = temperature =
`25^oC=[273+25]K=298K`

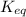`K_(eq)` = equilibrium constant at 25°C = 0.0632

Putting values in above equation, we get:

`\Delta G^o=-(8.314J/Kmol)* 298K* \ln (0.0632)\\\\\Delta G^o=6841.7J=6.84kJ`

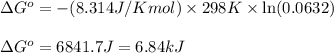
Hence, the standard Gibbs free energy of the given reaction is 6.84 kJ