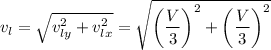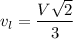Question

A watermelon is blown into three pieces by a large firecracker. Two pieces of equal mass m fly away perpendicular to one another, one in the x direction another in the y direction. Both of these pieces fly away with a speed of V = 42 m/s. The third piece has three times the mass of the other two pieces. Randomized Variables V = 42 m/s show answer No Attempt 33% Part (a) Write an expression for the speed of the larger piece, that is in terms of only the variable V.

Answer 1

Speed of larger piece is
`(V√(2))/(3)`

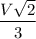
Step-by-step explanation:

We apply the principle of conservation of momentum.

The watermelon is initially at rest. The initial momentum = 0 kg m/s in all directions.

After the collision,

Vertical momentum = momentum of piece in y-direction + y-component of momentum of larger piece =
`mV + 3mv_(ly)`

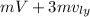
Here,
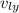`v_(ly)` is the y-component of velocity of larger piece.

This is equal to 0, since the initial momentum is 0.

`v_(ly)=(V)/(3)`

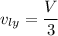
Horizontal momentum = momentum of piece in x-direction + x-component of momentum of larger piece =
`mV + 3mv_(lx)`

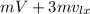
Here,
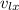`v_(lx)` is the x-component of velocity of larger piece.

This is also equal to 0, since the initial momentum is 0.

`v_(lx)=(V)/(3)`

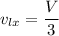
The velocity of the larger piece,
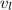`v_l`, is the resultant of
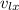`v_(lx)` and
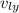`v_(ly)`. Since they are mutually perpendicular,

`v_l = \sqrt{v_(ly)^2+v_(lx)^2}= \sqrt{\left((V)/(3)\right)^2+\left((V)/(3)\right)^2}`

`v_l = (V√(2))/(3)`