Answer:
An investor is going to invest some amount of total investment in a risky portfolio which has the expected return of 17% and standard deviation of 27%. The remaining amount will be invested in the T-bills which has the expected return on 7%.
The risky portfolio includes stock A, stock B, and stock C.
By investing in risky portfolio and T-bills, the expected return on the portfolio will be 15%.
Proportion of risky portfolio in investors investment budget can be calculated by using the following equation:
![E(r_(c)) - r_(r) = y[E(r_(p) ) - r_(r) ]](https://img.qammunity.org/2021/formulas/business/college/g8ofk589hbm4cm4qo3qasu3wb5gqylgskt.png)
Here,
Risk-premium of client's overall portfolio is
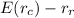
Risk-premium of client's risky portfolio is
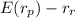
Expected return on client's overall portfolio is
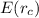
Expected return on client's risky portfolio is

Proportion of risky portfolio in client's overall portfolio is y.
Risk-free rate on Treasury bill is
This equation represents the relationship between risk-premium of risky portfolio, risk-premium of investor's overall portfolio and the proportion of risky portfolio in investor's overall portfolio.
Calculate the proportion of risky portfolio as follows:
![E(r_(c)) - r_(r) = y[E(r_(p) ) - r_(r) ]](https://img.qammunity.org/2021/formulas/business/college/g8ofk589hbm4cm4qo3qasu3wb5gqylgskt.png)
0.15 - 0.07 = y (0.17 - 0.07)
0.08 = y (0.10)
y = 0.08/0.10
Y = 0.80 (or) 80%
Hence, the proportion of risky portfolio in investor's overall portfolio (y) is 80%