Question

In a normally distributed data set with a mean of 24 and a standard deviation of 4.2, what percentage of the data would be between 15.6 and 32.4 and why?

Answer 1

About 95% of data lies between 15.6 and 32.4

Explanation:

We are given the following information in the question:

Mean, μ = 2.4

Standard Deviation, σ = 4.2

We are given that the distribution of SAT score is a bell shaped distribution that is a normal distribution.

Empirical Formula:

• Almost all the data lies within three standard deviation from the mean for a normally distributed data.
• About 68% of data lies within one standard deviation from the mean.
• About 95% of data lies within two standard deviations of the mean.
• About 99.7% of data lies within three standard deviation of the mean.

We have to find the percentage of data lying between 15.6 and 32.4

`15.6 = 24 - 2(4.2) = \mu - 2\sigma\\32.4 = 24 + 2(4.2) = \mu + 2\sigma`

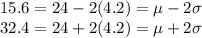
Thus, we have to find the percentage of data lying within two standard deviations of the mean. By Empirical formula about 95% of data lies between 15.6 and 32.4