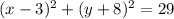Question

The diameter of a circle has endpoints (-2,-6) and (8,-10)

Enter an equation for the circle in standard form.

Answer 1

`(x - 3)^2 + (y + 8)^2 = 29` is equation for the circle in standard form

Solution:

Given that,

The diameter of a circle has endpoints (-2,-6) and (8,-10)

Use the midpoint formula to find center of circle

`C = ((x_1 + x_2)/(2) , (y_1+y_2)/(2))\\\\C = (( -2+8)/(2), (-6-10)/(2))\\\\C = (3, -8)`

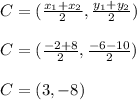
Radius = distance between center and one of end points

distance between (3 , -8) and (-2 , -6)

Use distance formula

`r = √((x2-x1)^2 + (y2-y1)^2)`

`r = √((-2-3)^2 + (-6+8)^2)\\\\r = √(25 + 4)\\\\r = √(29)`

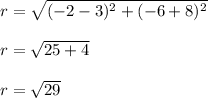
The standard equation of the circle:

`(x - h)^2 + (y-k)^2 = r^2`

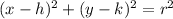
Where, (h , k) is the center of circle

`(x - 3)^2 + (y + 8)^2 = 29`

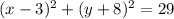
Thus the equation of circle is found