Answer:
2/7 or 0.2857
Explanation:
The expected time before the first bulb burns out (two bulbs working) is given by the inverse of the probability that a bulb will go out each day:
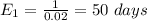
The expected time before the second bulb burns out (one bulb working), after the first bulb goes out, is given by the inverse of the probability that the second bulb will go out each day:
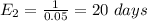
Therefore, the long-run fraction of time that there is exactly one bulb working is:

There is exactly one bulb working 2/7 or 0.2857 of the time.