Answer:
see explanation
Explanation:
A
Given
(x² + 3)² + 21 = 10x² + 30 ← factor out 10 from each term on the right side
(x² + 3)² + 21 = 10(x² + 3) ← subtract 10(x² + 3) from both sides
(x² + 3)² - 10(x² + 3) + 21 = 0
Substituting u = x² + 3 into the equation gives
u² - 10u + 21 = 0 → D
---------------------------------------------
B
Using u² - 10u + 21 = 0 to solve the equation
Consider the factors of the constant term (+ 21) which sum to give the coefficient of the u- term (- 10)
The factors are - 3 and - 7, since
- 3 × - 7 = 21 and - 3 - 7 = - 10, thus
(u - 3)(u - 7) = 0
Equate each factor to zero and solve for u
u - 3 = 0 ⇒ u = 3
u - 7 = 0 ⇒ u = 7
We now have to use the substitution to convert the solutions into terms of x, that is
x² + 3 = 3 ( subtract 3 from both sides )
x² = 0 ⇒ x = 0 → D
x² + 3 = 7 ( subtract 3 from both sides )
x² = 4 ( take the square root of both sides )
x = ±
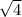 = ± 2
= ± 2
Thus x = - 2 → C
x = 2 → E