Question

A student takes a ten-question true-false quiz, but did not study and randomly guesses each answer. Find the probability that the student passes the quiz with a grade of at least 50% of the questions correct.

Answer 1

The probability of student passing the quiz with at least 50% of the questions correct is 0.62267.

Explanation:

Here, the total number of T/F question = 10

The minimum answers needed correctly answered = 50%

Now, 50% of 10 = 5 questions

So, student needs to answer at least 5 questions correctly.

Here, the possibility of answering a question correctly =
`(1)/(2)` = p = 0.5

Also, the possibility of answering a question wrong =
`(1)/(2)` = q = 0.5

Now, to pass he needs to answer 5 or more ( = 5, 6 , 7 , 8 , 9 or 10) answers correctly.

P(answering 5 correct answer) =
`^(10)C_5(0.5)^5(0.5)^5 =252 (0.5)^(10) = 0.246`

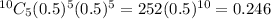
P(answering 6 correct answer) =
`^(10)C_6(0.5)^6(0.5)^4 =210 (0.5)^(10) = 0.2050`

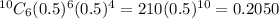
P(answering 7 correct answer) =
`^(10)C_7(0.5)^7(0.5)^3 =120 (0.5)^(10) = 0.1171`

P(answering 8 correct answer) =
`^(10)C_8(0.5)^8(0.5)^2 =120 (0.5)^(10) = 0.0439`

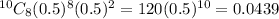
P(answering 9 correct answer) =
`^(10)C_9(0.5)^9(0.5)^1 = 0.0097`

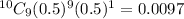
P(answering 10 correct answer) =
`^(10)C_(10)(0.5)^7(0.5)^3 =1 (0.5)^(10) = 0.00097`

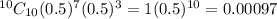
So, the total Probability

= (0.246) + (0.2050)+ (0.1171) +(0.0439) + (0.0097) + (0.00097)

= 0.62267 ≈ 62.2 %

Hence, the probability that the student passes the quiz with a grade of at least 50% of the questions correct is 0.62267.