Question

Prove algebraically what type of function this is (even, odd, or neither).

Answer 1

The given function is even.

Solution:

If f(-x) = f(x), then the function is even.

If f(-x) = -f(x), then the function is odd.

Given function:

`f(x)=x^(6)-x^(4)`

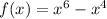
Substitute x = -x

`f(-x)=(-x)^(6)-(-x)^(4)`

`=x^(6)-x^(4)`

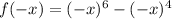
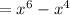
= f(x) (given)

f(-x) = f(x)

From the definition, it is even.

Hence the given function is even.