Question

Suppose that motorola uses the normal distribution to determine the probability of defects and the number of defects in a particular production process. Assume that the production process manufactures items with a mean weight of 10 ounces. Calculate the probability of a defect and the suspected number of defects for a 1

Answer 1

Explanation:

I think your question is lack of information, so here is my addition for it:

Motorola used the normal distribution to determine the probability of defects and the number of defects expected in a production process. Assume a production process produces items with a mean weight of 10 ounces. Calculate the probability of a defect and the expected number of defects for a 1000-unit production run in the following situations.

a,The process standard deviation is .15, and the process control is set at plus or minus one standard deviation. Units with weights less than 9.85 or greater than 10.15 ounces will be classified as defects.

My answer:

As we know that

μ = 10

σ = 0.15

The standarlized score is the value z decrease by the mean and then divided by the standard deviation.

Z = (x- μ) / σ =
`(9.85 -10)/(0,15)` ≈-1

Z = (x- μ) / σ =
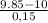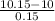`(10.15 -10)/(0.15)` ≈1

Determine the corresponding probability using the table 1 of the appendix

P (x<9.85 or x>10.15) = P(z < -1.00 or z > 1.00) = 2P9z<-1.00) = 2*0.1587 = 0.3714

She probability of a defect and the expected number of defects for a 1000-unit production = 0.3714 *100% = 37.14%