Question

The bottom of a double rainbow is going over a tree that is 18 feet tall if you're standing 20 feet from the tree what is the angle of elevation to the bottom of the rainbow

Answer 1

The angle of elevation to the bottom of the rainbow is 42°

Step-by-step explanation:

Given that the bottom of a double rainbow is going over a tree that is 18 feet tall and you're standing 20 feet from the tree.

We need to determine the angle of elevation to the bottom of the rainbow.

Let us use the trigonometric ratios to determine the angle of elevation.

Thus, we have,

`tan \ \theta=(opp)/(adj)`

where opp = 18 and adj = 20 and we need to determine the angle.

Substituting the values, we have,

`tan \ \theta=(18)/(20)`

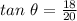
Dividing the values, we have,

`tan \ \theta=0.9`

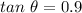
Taking
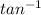`tan^{-1` on both sides of the equation, we get,

`\theta=tan^(-1)(0.9)`

Thus, we get,

`\theta=41.99^(\circ)`

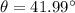
Rounding off to the nearest degree, we get,

`\theta=42^(\circ)`

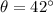
Hence, the angle of elevation to the bottom of the rainbow is 42°