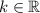Question

Please help ASAP

Find all the values of k so that the quadratic expression factors into two binomials. Explain the process used to find the values.

3x^2 + kx - 8

Answer 1

(-∞, ∞) or
`k \in \mathbb{R}`

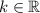
Explanation:

Binomial: two terms connected by a plus or minus sign.

Discriminant

`b^2-4ac\quad\textsf{when}\:ax^2+bx+c=0`

`\textsf{when }\:b^2-4ac > 0 \implies \textsf{two real roots}`

`\textsf{when }\:b^2-4ac=0 \implies \textsf{one real root}`

`\textsf{when }\:b^2-4ac < 0 \implies \textsf{no real roots}`

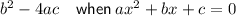
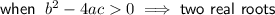
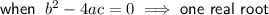
If a quadratic expression factors into two binomials, it will have two real roots. Therefore, the discriminant will be greater than zero.

Given quadratic expression:

`3x^2+kx-8`

`\implies a=3, \quad b=k, \quad c=-8`

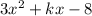
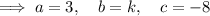
Substitute the values of a, b and c into the discriminant, set it to > 0:

`\implies k^2-4(3)(-8) > 0`

`\implies k^2+96 > 0`

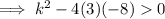
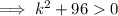
As k² ≥ 0 for all real numbers,

`\implies k^2+96 \geq 96`

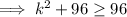
Therefore, the values of k are (-∞, ∞) or
`k \in \mathbb{R}`

Answer 2

• Any value of k

Explanation:

The quadratic expression can be factored into two binomials if it has two real roots.

Two real roots possible with non-negative discriminant:

• D ≥ 0

As D = b² - 4ac, we get the following inequality

• k² - 4(3)(-8) ≥ 0
• k² + 96 ≥ 0
• k² ≥ - 96

This is true for any value of k

• k ∈ (- ∞, + ∞)