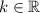Answer:
(-∞, ∞) or
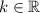
Explanation:
Binomial: two terms connected by a plus or minus sign.
Discriminant
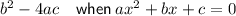
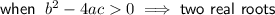
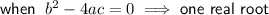
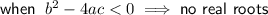
If a quadratic expression factors into two binomials, it will have two real roots. Therefore, the discriminant will be greater than zero.
Given quadratic expression:
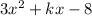
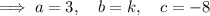
Substitute the values of a, b and c into the discriminant, set it to > 0:
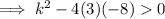
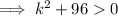
As k² ≥ 0 for all real numbers,
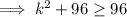
Therefore, the values of k are (-∞, ∞) or