Question

Solve f (x) = 32^x+6•1/2 = 8^x-1

Answer 1

Option B: The value of x is -16

Step-by-step explanation:

Given that the equation
`f(x)=32^(x+6) \cdot (1)/(2)=8^(x-1)`

We need to determine the value of x.

Let us substitute f(x) = 0, then we have,

`32^(x+6) \cdot (1)/(2)=8^(x-1)`

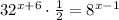
Now, we shall determine the value of x.

The term
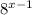`8^(x-1)` can be written as
`\left(2^(3)\right)^(x-1)`

Hence, we have,

`32^(x+6) \cdot (1)/(2)=\left(2^(3)\right)^(x-1)`

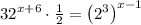
Also, the term
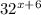`32^(x+6)` can be written as
`\left(2^(5)\right)^(x+6)`

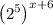
Thus, we have,

`\left(2^(5)\right)^(x+6) (1)/(2)=\left(2^(3)\right)^(x-1)`

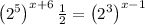
Applying the exponent rule,
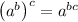`\left(a^(b)\right)^(c)=a^(b c)`, we have,

`2^(5(x+6)) \cdot (1)/(2)=2^(3(x-1))`

`2^(5(x+6)) \cdot 2^(-1)=2^(3(x-1))`

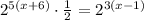
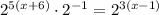
If
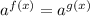`a^(f(x))=a^(g(x))` then
`f(x)=g(x)`

`5(x+6)-1=3(x-1)`

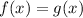
Simplifying, we get,

`5x+30-1=3x-3`

`5x+29=3x-3`

`2x+29=-3`

`2x=-32`

`x=-16`

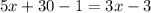
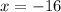
Therefore, the value of x is -16

Hence, Option B is the correct answer.