Question

Select the solution to the graph from the following points. Select all that apply.

Answer 1

The solutions are:

(-15 , -4) ⇒ 1st

(3 , 2) ⇒ 3rd

(21 , 8) ⇒ 5th

Explanation:

To find the solution of the graph let us make the equation of the line by using any two points on the line

The form of the linear equation is y = m x + b, where

• m is the slope of the line
• b is the y-intercept (value y at x = 0)

The formula of the slope is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

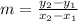
From the figure

∵ The line passes through points (-3 , 0) and (0 , 1)

- Find the slope of the line

∴
`m=(1-0)/(0--3)=(1)/(3)`

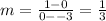
- Substitute the value of m in the form of the equation

∴ y =
`(1)/(3)` x + b

∵ b is the value of y at x = 0

∵ y = 1 at x = 0 ⇒ y-intercept

∴ b = 1

∴ y =
`(1)/(3)` x + 1

Lets substitute the x-coordinate of each point to find the y-coordinate, if the y-coordinate is equal to the y-coordinate of the points, then the point is a solution

Point (-15 , -4)

∵ x = -15

∴ y =
`(1)/(3)` (-15) + 1

∴ y = -5 + 1 = -4 ⇒ same value of the point

∴ (-15 , -4) is a solution

Point (-6 , 1)

∵ x = -6

∴ y =
`(1)/(3)` (-6) + 1

∴ y = -2 + 1 = -1 ⇒ not the same value of the point

∴ (-6 , 1) is not a solution

Point (3 , 2)

∵ x = 3

∴ y =
`(1)/(3)` (3) + 1

∴ y = 1 + 1 = 2 ⇒ same value of the point

∴ (3 , 2) is a solution

Point (12 , 9)

∵ x = 12

∴ y =
`(1)/(3)` (12) + 1

∴ y = 4 + 1 = 5 ⇒ not the same value of the point

∴ (12 , 9) is not a solution

Point (21 , 8)

∵ x = 21

∴ y =
`(1)/(3)` (21) + 1

∴ y = 7 + 1 = 8 ⇒ same value of the point

∴ (21 , 8) is a solution