Answer:
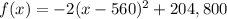
or

Explanation:
Let
f(x) ----> the profit earned
x ---> is the number of orders fulfilled
we know that
The equation of a quadratic equation in vertex form is equal to
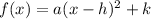
where
a is the leading coefficient of the quadratic equation
(h,k) is the vertex
Remember that
The x-intercepts or roots are the values of x when the value of the function is equal to zero
In this problem
The x-intercepts are
x=240 and x=880
The x-coordinate of the vertex (h) is the midpoint of the roots
so
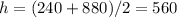
The y-coordinate of the vertex (k) is the maximum profit earned
 ----> is given
----> is given
so
The vertex is the point (560,204,800)
substitute in the quadratic equation
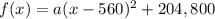
Find the value of a
we have the ordered pairs (240,0) and (880,0) (the x-intercepts)
take the point (240,0) and substitute the value of x and the value of y in the quadratic equation
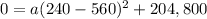
solve for a

therefore
The function that models the profits of the company is given by
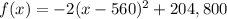 ----> equation in vertex form
----> equation in vertex form
Convert to standard form


