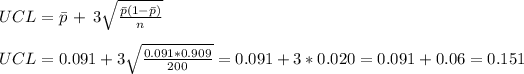Question

A sample of 200 ROM computer chips was selected on each of 30 consecutive days, and the number of nonconforming chips on each day was as follows: 8, 19, 27, 17, 38, 18, 4, 27, 9, 22, 30, 17, 14, 23, 15, 14, 12, 20, 13, 18, 14, 20, 9, 27, 30, 13, 10, 19, 12, 26. Construct a p chart and examine it for any out-of-control points. (Round your answers to four decimal places.)

p =
LCL =
UCL=

Comment on the chart.

The value of s on the 5th day lies below the LCL, so an out-of-control signal is generated.

The value of s on the 5th day lies above the UCL, so an out-of-control signal is generated.

Most points are between these limits, so the process appears to be in control with respect to variability.

All points are between these limits, so the process appears to be in control.

All points are between these limits, so the process appears to be out of control.

Answer 1

p = 0.091

LCL = 0.031

UCL= 0.151

The value of s on the 5th day lies below the LCL, so an out-of-control signal is generated. FALSE

The value of s on the 5th day lies above the UCL, so an out-of-control signal is generated. TRUE. This point is above the UCL and therefore out of the control limits, so its an statistically abnormal value.

Most points are between these limits, so the process appears to be in control with respect to variability. TRUE. Most of the points are between the LCL and the UCL, which is expected because the limits are calculated based on this very same data points.

All points are between these limits, so the process appears to be out of control. FALSE. The process is out of control when the points start to be outside of the limits.

Explanation:

We have samples of 200 chips from 30 consecutive days.

The number of non-conforming chips on each day is: 8, 19, 27, 17, 38, 18, 4, 27, 9, 22, 30, 17, 14, 23, 15, 14, 12, 20, 13, 18, 14, 20, 9, 27, 30, 13, 10, 19, 12, 26.

The limits of control (upper and lower) are calculated as:

`\bar p \,\pm\,3\sqrt{(\bar p (1- \bar p))/(n) }`

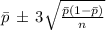
This gives a 3 standard deviation range both above and below the average proportion to know which values are statistically normal and which are abnormal.

The proportion in the long term will be estimated based on the 30-day data because there is no other better information. This is done calculating the proportion for every sample (dividing by 200) and then calculating the average of the proportions.

The value is then:

`\bar p=0.091`

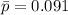
The lower control limit LCL is:

`LCL=\bar p \,-\,3\sqrt{(\bar p (1- \bar p))/(n) }\\\\LCL=0.091-3\sqrt{(0.091 *0.909)/(200) }=0.091-3*0.020 =0.091-0.060=0.031`

The upper control limit UCL is:

`UCL=\bar p \,+\,3\sqrt{(\bar p (1- \bar p))/(n) }\\\\UCL=0.091+3\sqrt{(0.091 *0.909)/(200) }=0.091+3*0.020 =0.091+0.06=0.151`