Question

Solve x2+4x+6=0 by graphing

Answer 1

Answer: x = -2±√2 i or no real roots. See the explanation below.

Explanation:

If you draw the graph, you will notice that there are no common points or you can say that there are no x-intercepts.

This means that the equation doesn't have any real roots.

If there are 2 common points (2 x-intercepts) then there are 2 real roots (answers.)

If there is only one common point (vertex is on x-axis) then there is only 1 real root.

If there aren't any common points (no x-intercepts) then there are no real roots.

So first, I'm gonna convert the equation into function and convert the standard form to vertex form.

`x^2+4x+6=0\\y=x^2+4x+6\\y=(x^2+4x+4)-4+6\\y=(x+2)^2+2`

We notice that the vertex is at (-2,2), the graph doesn't have x-intercepts (Graph below)

So the answer is clearly complex.

If you solve this by solving the equation then it'll be.

`x^2+4x+6=0\\x= (-b+-√(b^2-4ac))/(2a) \\x=(-4+-√(16-24) )/(2)\\x=(-4+-√(-8) )/(2)\\\\x=(-4+-2√(2)i )/(2)\\\\x={-2+-1√(2)i }\\\\`

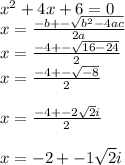
The answer is complex.

However, you can find the value of x easily by graphing. For example.

`x^2+6x+5=0`

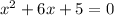
Factor then you get

`(x+5)(x+1)=0\\x=-5,-1`

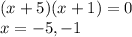
Or you can convert it to vertex form then graph.

`y=x^2+6x+5`

`y=(x^2+6x+9)-9+5\\y=(x+3)^2-4`

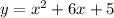
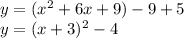
The vertex is at (-3,-4) then graph parabola (x-intercepts determine the roots of quadratic equation. For the graph, parabola intercepts x at (-5,0) and (-1,0) that means both -5 and -1 both are the value of x.

Note:

From the standard form,
`y=ax^2+bx+c` The graph is called Parabola, and it's Quadratic Function.

a is how the graph is, for example. If a>0, the graph is supine parabola and if a<0 then the graph is inverted parabola.

|a| is determined if the graph is wide or narrow, the more the value of a is, the more narrow it will be. The less the value of a is, the more wide it will be.

b is what determined the change of graph (likely vertex). Without b, then it'd be
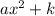`ax^2+k` which only move y-axis and not x-axis.

c is what determined the y-intercept and y-axis. If there is no b or the value of b is 0 then the vertex is at (0,c). If there is the value of b then c is only determined the y-intercept.