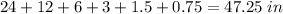Question

A student cuts pieces of ribbon to decorate a banner the first piece of ribbon is 24 inches long. The next piece of ribbon is one-half the length of the piece before, and so on. What is the total length of the first 6 pieces of ribbon?

A) 0.75
B) 1.5
C) 23.25
D) 47.25

Answer 1

Option D) 47.25 in

Explanation:

we know that

The equation of a exponential decay function is equal to

`y=a(1-r)^x`

where

y is the total length

x is the number of pieces of ribbon

a is the initial value

r is the rate of change

we have

`a=24\ in\\r=50\%=50/100=0.50`

substitute

`y=24(1-0.50)^x`

`y=24(0.50)^x`

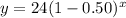
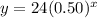
we have that

For x=0 ----->
`y=24\ in`

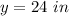
For x=1 ---->
`y=24(0.50)^1=12\ in`

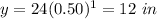
For x=2 ---->
`y=24(0.50)^2=6\ in`

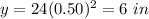
For x=3 ---->
`y=24(0.50)^3=3\ in`

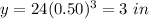
For x=4 ---->
`y=24(0.50)^4=1.5\ in`

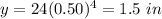
For x=5 ---->
`y=24(0.50)^5=0.75\ in`

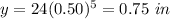
Adds the length of the first 6 pieces of ribbon

`24+12+6+3+1.5+0.75=47.25\ in`