Answer:
f(x) = {x-3 for x ≤ -1; -3x+14 for x > 5}
Explanation:
To write the piecewise function, we can consider the pieces one at a time. For each, we need to define the domain, and the functional relation.
__
Left Piece
The domain is the horizontal extent. It is shown as -∞ to -1, with -1 included.
The relation has a slope (rise/run) of +1, and would intersect the y-axis at -3 if it were extended.
The first piece can be written ...
f(x) = x-3 for x ≤ -1
__
Right Piece
The domain is shown as 5 to ∞, with 5 not included.
The relation is shown as having a slope (rise/run) of (-3)/(1) = -3. If extended, it would intersect the point (5, -1), so we can write the point-slope equation as ...
y -(-1) = -3(x -5)
y = -3x +15 -1 = -3x +14
The second piece can be written ...
f(x) = -3x +14 for x > 5
__
Whole function
Putting these pieces together, we have ...
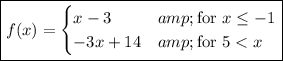
_____
Additional comment
Sometimes it is convenient to write inequalities in number-line order (using < or ≤ symbols). This gives a visual indication of where the variable stands in relation to the limit(s). Perhaps a more conventional way to write the domain for the second piece is, x > 5.