Question

Suppose that 20% of the residents in a certain state support an increase in the property tax. An opinion poll will randomly sample 400 state residents and will then compute the proportion in the sample that support a property tax increase. How likely is the resulting sample proportion, ^ p , to be within 0.04 of the true proportion, p (i.e., between 0.16 and 0.24)

Answer 1

P(0.16 <
`\hat p` < 0.24) = 0.9546 or 95.5%

Explanation:

We are given that 20% of the residents in a certain state support an increase in the property tax. An opinion poll will randomly sample 400 state residents and will then compute the proportion in the sample that support a property tax increase.

Let p = % of the residents in a certain state that support an increase in the property tax = 20%

`\hat p` = % of the residents in a certain state that support an increase in the

property tax in a sample of 400 residents

The one-sample z sore probability distribution for sample proportion is given by;

Z =
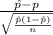`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }` ~ N(0,1) where, n = sample residents = 400

So, probability that sample proportion will lie between 0.16 and 0.24 is given by = P(0.16 <
`\hat p` < 0.24)

P(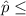0.16 <
`\hat p` < 0.24) = P(
`\hat p` < 0.24) - P(
`\hat p \leq` 0.16)

P(
`\hat p` < 0.24) = P(
`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }` <
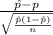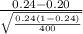`\frac{0.24 -0.20}{\sqrt{(0.24(1- 0.24))/(400) } }` ) = P(Z < 1.87) = 0.96926

P(
`\hat p`
`\leq` 0.16) = P(
`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }`
`\leq`
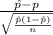
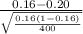`\frac{0.16 -0.20}{\sqrt{(0.16(1- 0.16))/(400) } }` ) = P(Z < -2.18) = 1 - P(Z
`\leq` 2.18)

= 1 - 0.98537 = 0.01463

Therefore, P(0.16 <
`\hat p` < 0.24) = 0.96926 - 0.01463 = 0.9546

Hence, it is 95.5% likely that the sample proportion will lie between 0.16 and 0.24.

Answer 2

Roughly a 95% chance.

Explanation:

The standard deviation of sample of size 'n' and with a proportion 'p' is given by:

`SD = \sqrt{(p*(1-p))/(n) }`

In this case, in a sample of 400 residents with proportion 20%, the standard deviation is:

`SD=\sqrt{(0.2*(1-0.2))/(400) }\\ SD=0.02`

The upper and lower limits proposed (0.16 and 0.24) are exactly two standard deviations above and below the mean of 0.20. According to the 95% rule, this interval comprehends 95% of all data. Therefore, there is roughly a 95% chance that the resulting sample proportion will be within 0.04 of the true proportion.