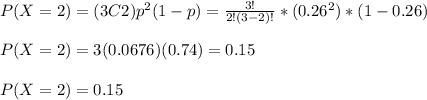Answer:
(a)
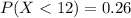
(b)
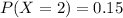
Explanation:
Question a
This is a Poisson distribution. The average/mean, μ = 14
So, probability that fewer than 12 field mice are found on a given acre is:

Question b
This is a Binomial distribution with:
Probability of success, p = 0.26
n = 3