Question

A publisher reports that 26&% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 220220 found that 20 % of the readers owned a laptop. Find the value of the test statistic. Round your answer to two decimal places.

Answer 1

Test statistics = -2.22

Explanation:

We are given that a publisher reports that 26% of their readers own a laptop. A random sample of 220 found that 20% of the readers owned a laptop.

And, a marketing executive wants to test the claim that the percentage is actually different from the reported percentage, i.e;

Null Hypothesis,
`H_0` : p = 0.26 {means that the percentage of readers who own a laptop is same as reported 26%}

Alternate Hypothesis,
`H_1` : p
`\\eq` 0.26 {means that the percentage of readers who own a laptop is different from the reported 26%}

The test statistics we will use here is;

T.S. =
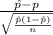`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }` ~ N(0,1)

where, p = actual percentage of readers who own a laptop = 0.26

`\hat p` = percentage of readers who own a laptop in a sample of

220 = 0.20

n = sample sizes = 220

So, Test statistics =
`\frac{0.20 -0.26}{\sqrt{(0.20(1- 0.20))/(220) } }`

= -2.22

Therefore, the value of test statistics is -2.22 .