Question

Factor completely 3x^3-6x^2-24x

Answer 1

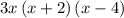`3x\left(x+2\right)\left(x-4\right)\\` is the required form.

Explanation:

We have to find the factor of the expression, that is given in the question. So for that, we have to first find the common term, and then apply the middle term split method. There are various other ways to do it too.

Now the expression that is given to us is:

`3x^3-6x^2-24x\\`

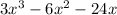
So here we will take x common and we will get:

`3x^3-6x^2-24x\\=3x\left(x^2-2x-8\right)\\`

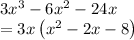
Now we will do the middle term split as follows:

`3x\left(x^2-2x-8\right)\\=3x\left ( \left(x^2+2x\right)+\left(-4x-8\right) \right )\\=3x\left(x+2\right)\left(x-4\right)\\`

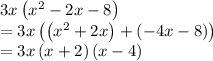
after taking the common term. So this is the required factor form of the given expression.