Question

One of the earliest applications of the Poisson distribution was in analyzing incoming calls to a telephone switchboard. Analysts generally believe that random phone calls are Poisson distributed. Suppose phone calls to a switchboard arrive at an average rate of 3.0 calls per minute. a. If an operator wants to take a one-minute break, what is the probability that there will be no calls during a one-minute interval? b. If an operator can handle at most five calls per minute, what is the probability that the operator will be unable to handle the calls in any one-minute period? c. What is the probability that exactly three calls will arrive in a two-minute interval? d. What is the probability that one or fewer calls will arrive in a 30-second interval?

Answer 1

(a) P (X = 0) = 0.0498.

(b) P (X > 5) = 0.084.

(c) P (X = 3) = 0.09.

(d) P (X ≤ 1) = 0.5578

Explanation:

Let X = number of telephone calls.

The average number of calls per minute is, λ = 3.0.

The random variable X follows a Poisson distribution with parameter λ = 3.0.

The probability mass function of a Poisson distribution is:

`P(X=x)=(e^(-\lambda)\lambda^(x))/(x!);\ x=0,1,2,3...`

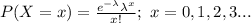
(a)

Compute the probability of X = 0 as follows:

`P(X=0)=(e^(-3)3^(0))/(0!)=(0.0498*1)/(1)=0.0498`

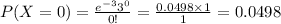
Thus, the probability that there will be no calls during a one-minute interval is 0.0498.

(b)

If the operator is unable to handle the calls in any given minute, then this implies that the operator receives more than 5 calls in a minute.

Compute the probability of X > 5 as follows:

P (X > 5) = 1 - P (X ≤ 5)

`=1-\sum\limits^(5)_(x=0) { (e^(-3)3^(x))/(x!)} \,\\=1-(0.0498+0.1494+0.2240+0.2240+0.1680+0.1008)\\=1-0.9160\\=0.084`

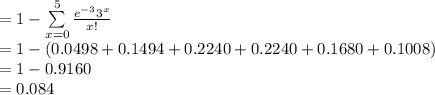
Thus, the probability that the operator will be unable to handle the calls in any one-minute period is 0.084.

(c)

The average number of calls in two minutes is, 2 × 3 = 6.

Compute the value of X = 3 as follows:

`P(X=3)=(e^(-6)6^(3))/(3!)=(0.0025*216)/(6)=0.09`

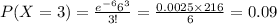
Thus, the probability that exactly three calls will arrive in a two-minute interval is 0.09.

(d)

The average number of calls in 30 seconds is, 3 ÷ 2 = 1.5.

Compute the probability of X ≤ 1 as follows:

P (X ≤ 1 ) = P (X = 0) + P (X = 1)

`=(e^(-1.5)1.5^(0))/(0!)+(e^(-1.5)1.5^(1))/(1!)\\=0.2231+0.3347\\=0.5578`

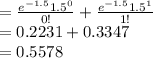
Thus, the probability that one or fewer calls will arrive in a 30-second interval is 0.5578.