Question

(1 point) Urn A has 5 white and 17 red balls. Urn B has 9 white and 12 red balls. We flip a fair coin. If the outcome is heads, then a ball from urn A is selected, whereas if the outcome is tails, then a ball from urn B is selected. Suppose that a white ball is selected. What is the probability that the coin landed heads

Answer 1

The probability that the coin landed heads is 65.3%.

Explanation:

Given : Urn A has 5 white and 17 red balls. Urn B has 9 white and 12 red balls. We flip a fair coin. If the outcome is heads, then a ball from urn A is selected, whereas if the outcome is tails, then a ball from urn B is selected. Suppose that a white ball is selected.

To find : What is the probability that the coin landed heads ?

Solution :

Let the event A be the ball taken from Urn A (5 white and 17 red balls)

Let B=A'- the ball taken from urn B(9 white and 12 red balls)

Let W be event that a white ball is selected.

An urn is chosen based on a toss of a fair coin.

P(A) = coin landed on heads =
`(1)/(2)`

P(B) = coin landed on tails =
`P(A')=(1)/(2)`

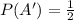
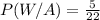`P(W/A)=(5)/(22)` and
`P(W/B)=(3)/(7)`

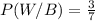
Using Bayes formula,

`P(B/W)=(P(W/B)P(B))/(P(W/B)P(B)+P(W/A)P(A))`

`P(B/W)=((3)/(7)* (1)/(2))/((3)/(7)* (1)/(2)+(5)/(22)* (1)/(2))`

`P(B/W)=((3)/(14))/((3)/(14)+(5)/(44))`

`P(B/W)=((3)/(14))/((132+70)/(14* 44))`

`P(B/W)=((3)/(14))/((202)/(616))`

`P(B/W)=(3* 616)/(14* 202)`

`P(B/W)=(66)/(101)`

`P(B/W)=65.3\%`

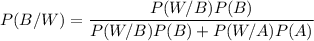
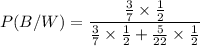
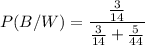
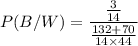
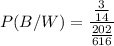
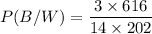
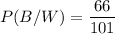
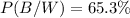
Therefore, the probability that the coin landed heads is 65.3%.